Algebra 2

Also known as "College Algebra"

OK. So what are you going to learn here?

You will learn about Numbers, Polynomials, Inequalities, Sequences and Sums, many types of Functions, and how to solve them.

You will also gain a deeper insight into Mathematics, get to practice using your new skills with lots of examples and questions, and generally improve your mind.

With your new skills you will be able to put together mathematical models so you can find good quality solutions to many tricky real world situations.

Near the end of most pages is a "Your Turn" section ... do these! You need to balance your reading with doing. Answering questions helps you sort things out in your mind. And don't guess the answer: use pen and paper and try your best before seeing the solution.

Language

So what is this thing called Mathematics? And how do you go about learning it?

Reading Math

  • Welcome to Mathematics
  • Learning Mathematics
  • The Language of Mathematics
  • Symbols in Algebra

Sets

Next, we need to think about mathematics in terms of sets.

set

  • Introduction to Sets

Numbers

Now we know what a set is, let us look at different sets of numbers that are useful:

  • The Evolution of Numbers
  • Prime and Composite Numbers
  • Fundamental Theorem of Arithmetic
  • Whole Numbers and Integers

pi symbol

  • Rational Numbers
  • Using Rational Numbers
  • Irrational Numbers
  • 0.999... = 1
  • Real Numbers

square root of minus one

  • Imaginary Numbers
  • Complex Numbers
  • Multiplying Complex Numbers
  • The Complex Plane

  • Common Number Sets

Inequalities

"Equal To" is nice but not always available. Maybe we only know that something is less than, or greater than. So let's learn about inequalities.

a≥b

  • Introduction to Inequalities
  • Properties of Inequalities
  • Solving Inequalities
  • Solving Inequality Word Questions
  • Intervals

Exponents

We will be using exponents a lot, so let's get to know them well.

8 to the Power 2

  • Exponents
  • Variables with Exponents
  • Using Exponents in Algebra
  • Squares and Square Roots
  • Squares and Square Roots in Algebra
  • nth Root
  • Fractional Exponents
  • Laws of Exponents
  • Exponents of Negative Numbers

Polynomials

Polynomials were some of the first things ever studied in Algebra. They are simple, yet powerful in their ability to model real world situations.

polynomial example

  • What is a Polynomial?
  • Adding And Subtracting Polynomials
  • Multiplying Polynomials
  • Polynomials - Long Multiplication
  • Dividing Polynomials
  • Polynomials - Long Division

  • Degree (of an Expression)
  • Special Binomial Products
  • Difference of Two Cubes

expand vs factor

  • Factoring in Algebra
  • Solving Polynomials
  • Roots of Polynomials: Sums and Products

  • Rational Expressions
  • Using Rational Expressions

  • Fundamental Theorem of Algebra
  • Remainder Theorem and Factor Theorem
  • General Form of a Polynomial

Graphing Polynomials

  • How Polynomials Behave
  • Polynomials: The Rule of Signs
  • Polynomials: Bounds on Zeros

Equations

And, of course, we need to know about equations ... and how to solve them.

  • Equations and Formulas
  • Solving Equations
  • Simplify
  • Solving Word Questions
  • Zero Product Property
  • Implication and Iff
  • Theorems, Corollaries, Lemmas

Graphs

Graphs can save us! They are a great way to see what is going on and can help us solve many things. But we need to be careful, as they sometimes don't give the full story.

Intercepts

  • Cartesian Coordinates
  • Pythagoras' Theorem
  • Distance Between 2 Points
  • Graph of an Equation
  • Finding Intercepts From an Equation
  • Symmetry in Equations

Linear Equations

They are just equations for lines. But they come in many forms.

Slope-Intercept Form

  • Equation of a Straight Line
  • Linear Equations
  • Point-Slope Equation of a Line
  • General Form of Equation of a Line
  • Equation of a Line from 2 Points
  • Midpoint of a Line Segment
  • Parallel and Perpendicular Lines

Functions

A function relates an input to an output. But from that simple foundation many useful things can be built.

doman and range

  • What is a Function?
  • Domain, Range and Codomain

  • Evaluating Functions

  • Increasing and Decreasing Functions
  • Maxima and Minima of Functions
  • Even and Odd Functions
  • Set-Builder Notation

  • Common Functions Reference:

    • Square Function
    • Square Root Function
    • Cube Function
    • Reciprocal Function
    • Absolute Value Function
    • Floor and Ceiling Function

  • Function Transformations
  • Equation Grapher
  • Operations with Functions
  • Composition of Functions
  • Inverse Functions

Equations of Second Degree

"Second degree" just means the variable has an exponent of 2, like x2. It is the next major step after linear equations (where the exponent is 1, like x).

Quadratic Graph

  • Quadratic Equations
  • Factoring Quadratics
  • Completing the Square
  • Derivation of Quadratic Formula
  • Graphing Quadratic Equations
  • Quadratic Equations in the Real World
  • Circle Equations

Solving

We already have experience in solving, but now we can learn more!

3d Box

  • Mathematical Models and Mathematical Models 2
  • Approximate Solutions
  • Intermediate Value Theorem
  • Solving Radical Equations
  • Change of Variables
  • Algebra Mistakes

Solving Inequalities

We learned about inequalities above, now let's learn how to solve them.

  • Solving Inequalities
  • Graphing Linear Inequalities
  • Inequality Graphing Tool
  • Solving Quadratic Inequalities
  • Solving Rational Inequalities
  • Absolute Value in Algebra

Exponents and Logarithms

We already know about exponents ... well logarithms just go the other way. And together they can be very powerful.

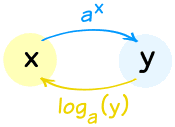
Exponent vs Logarithm

  • Introduction to Logarithms
  • Exponents, Roots and Logarithms
  • Working with Exponents and Logarithms
  • Exponential Function
  • Logarithmic Function
  • Exponential Growth and Decay

Systems of Linear Equations

What happens when we have two or more linear equations that work together? They can often be solved! It isn't very hard but can take a lot of calculations.

A Matrix

  • Systems of Linear Equations

  • Matrices
  • Types of Matrix
  • How to Multiply Matrices
  • Determinant of a Matrix
  • Inverse of a Matrix:
    • Using Elementary Row Operations (Gauss-Jordan)
    • Using Minors, Cofactors and Adjugate
  • Scalar, Vector, Matrixand Vectors
  • Matrix Calculator
  • More at Matrix Index

  • Solving Systems of Linear Equations Using Matrices

  • Systems of Linear and Quadratic Equations

Probability

lock

Is it likely? You be the judge!

  • Probability
  • The Basic Counting Principle
  • Combinations and Permutations

Sequences, Series and Partial Sums

A Sequence is a set of things (usually numbers) that are in order. We can also sum up a series, where Sigma Notation is very useful.

sequence term

  • Sequences
  • Sequences - Finding A Rule
  • Sigma Notation
  • Partial Sums
  • Arithmetic Sequences and Sums
  • Geometric Sequences and Sums

Finally

These last few subjects use what we have learned above.

  • Partial Fractions
  • Mathematical Induction
  • Pascal's Triangle
  • Binomial Theorem

And that is all!

But there are many other interesting algebra topics such as:

  • Euler's Formula for Complex Numbers
  • Taylor Series (needs a basic understanding of derivatives)